Linear Transformations Explained with 5 Examples

October 2, 2023

Most of us are familiar with the function of y = x. This is a parent function (the core representation of that type of function) for a linear equation. However, when we start exploring how these equations would represent real life, not all of them will be represented by the parent function y = x. They will be changed through linear transformations, which come in multiple forms. Here, we will explore the various forms of linear transformations in written and graphical form.

 

Vertical Shift

 

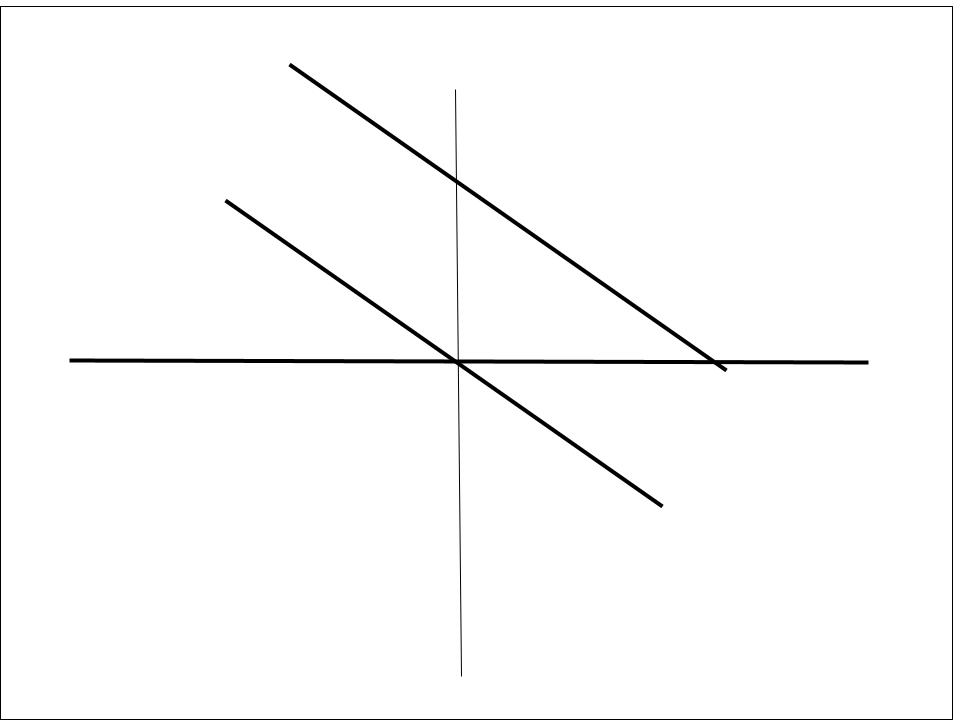
Example 1

 

Example 2

 

This type of linear transformation will move the linear function vertically, either in a positive or negative direction. This linear transformation will be associated with the y-intercept of the function. As seen in the examples above, there is one equation with a positive vertical shift, as well as another with a negative vertical shift. The slope may be the same, but the outputs associated with the inputs will either increase or decrease depending on the value of the new y-intercept given. The direction goes in the same way as the sign.

 

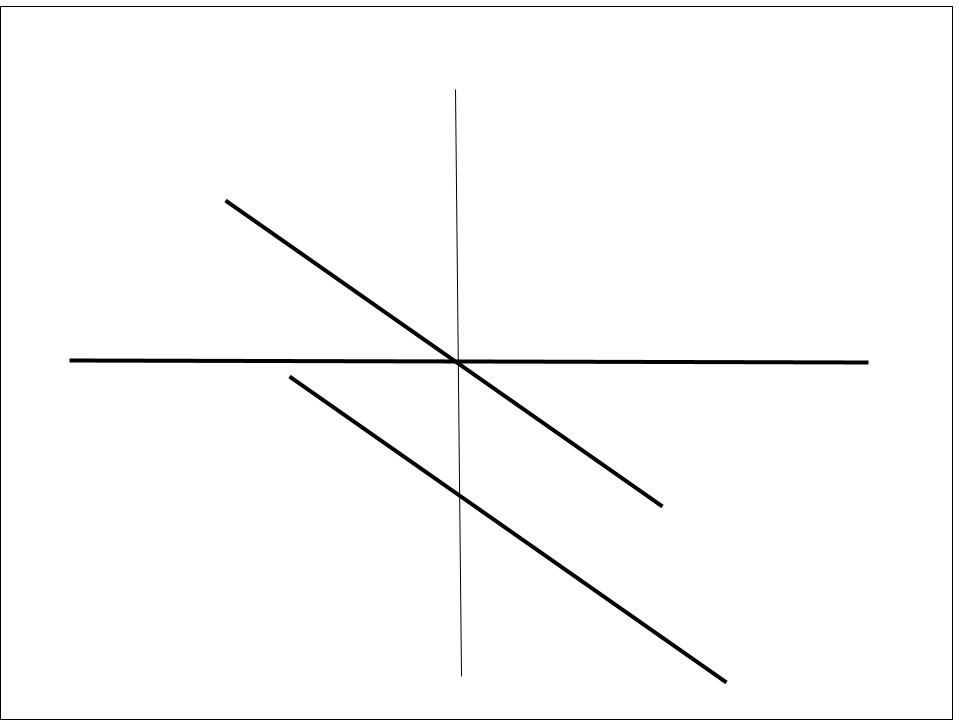
Vertical Stretch and Compression

 

Example 3

 

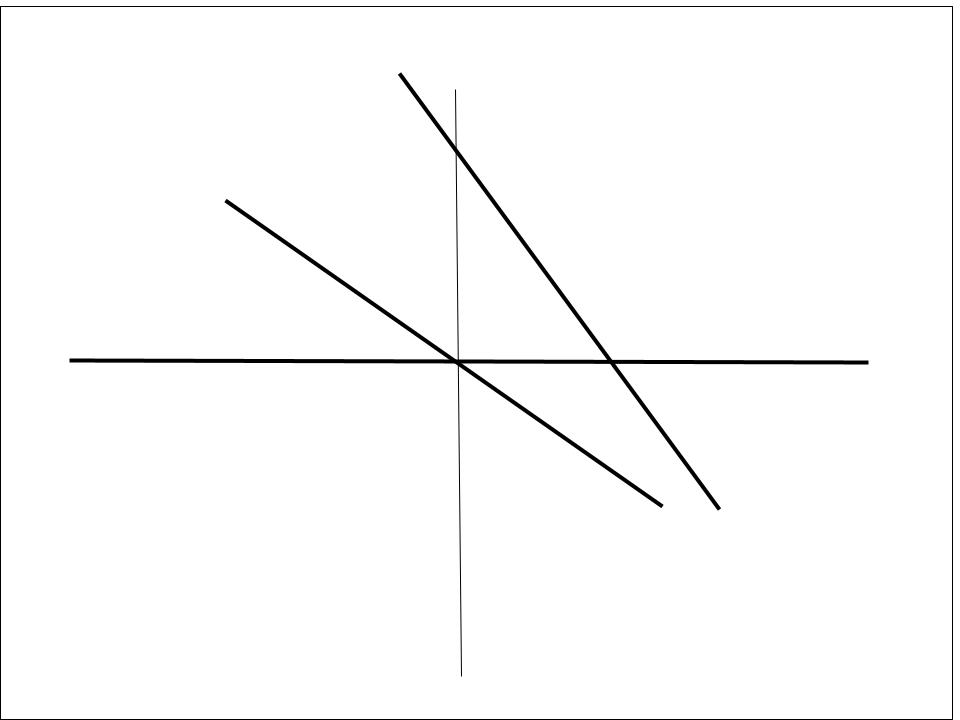
Example 4

 

Example 5

 

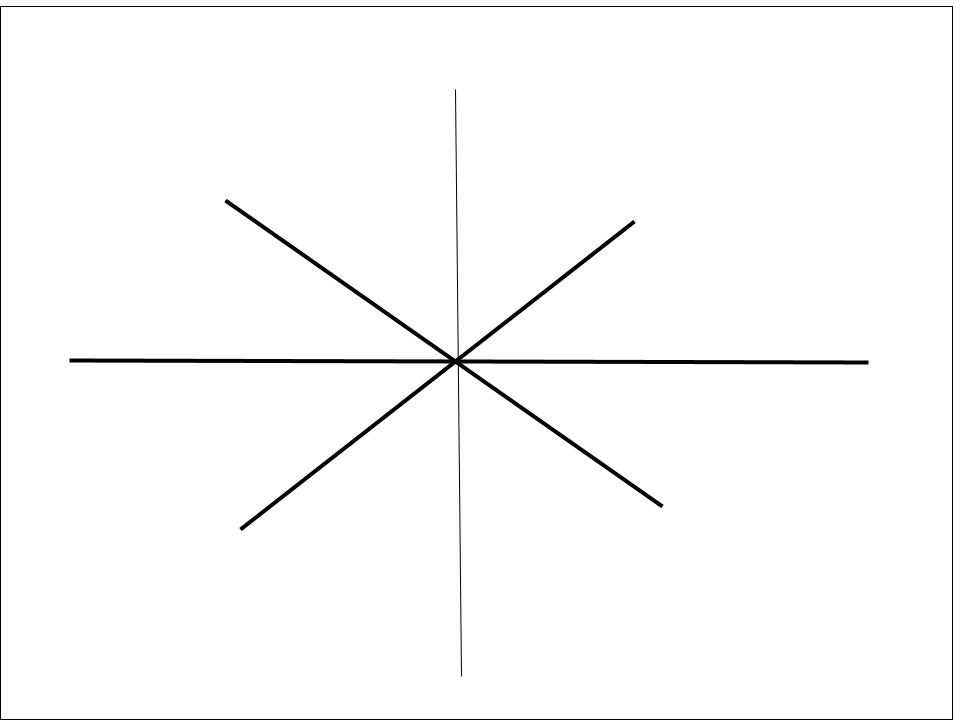
While the parent function is often represented as y=x, the slope-intercept form is written as y = mx + b. The “m” represents the slope and has the biggest influence on whether a stretch or compression transformation has been done. The way you can tell is by looking at the number representing m. If the absolute value of the number representing m is less than one more than zero and smaller than the previous “m”, the function will be compressed. Visually this means it will look closer to resembling a horizontal line. If the value is larger than one, this line will appear more vertical and steeper, indicating that a vertical stretch transformation has occurred. The reason the negative sign does not play a role in the stretching or compression of a linear function is that the negative sign is only involved in reflecting the y-values in question. This means that for all the x-values in question, the y-values that correspond to the original equation will all have negative values.

 

Why Do Linear Transformations Matter?

 

Linear functions can be used in many fields to help extrapolate or interpolate important information. It can be used to estimate money earned over a period of time, miles traveled, and the steepness of a ski slope, among many other things. Transformations come into play because the way a y-intercept shifts or the way a slope changes will impact the entire equation and its corresponding graph. As we explore further into advanced levels of linear algebra, linear transformations play a more complex role in understanding high-dimensional planes. Our primary reason for understanding linear transformations is to help us solve systems of linear equations. However, in fields such as computer science or physics, they can also become depicted as matrices or vectors. The way this works is that they are stacked with x on top and y on the bottom. The leftwards direction is represented with a negative sign on the x-value and the right is positive. Like with traditional linear equations, the y-value is represented consistently with a positive value representing an upward shift and a negative value representing a downward shift.

 

Vectors can be represented in matrix form as well and can be used to perform linear transformations in planes beyond the third dimension, but if you know the primary fundamentals of linear transformations, then you have the foundation to understand the advanced implications as well.

 

 

Author: Maaida Kirmani