The slope of a line measures the steepness in which a linear equation ascends or descends. Mathematically, this can be calculated by the ratio of the “rise over run,” which is the change in the y value divided by the change in the x value. There are three ways in which you can find the slope of a line.

1. Finding the slope (m) from a graph using slope formula:
When the graph of a line is given, the slope can be found by finding two points that the line passes through. In the picture to the left, the line passes through point (0, 5) and point (4, 2). Once the two points have been determined, count the number of units vertically and horizontally. Then use the slope formula:
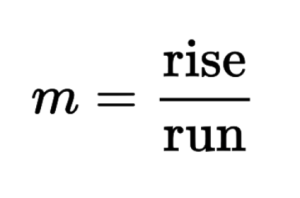
so, the slope of this line is -3/4.
2. Finding the slope (m) from two points:
When there are two known points that fall on a line, the slope can be found by finding the distance between each point and then dividing. Let’s use the same two points from the graph above: (0, 5) and (4, 2).
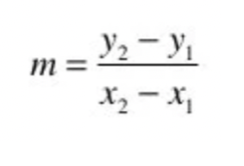
so, m = (2-5) / (4-0) = -3/4.
3. Finding the slope (m) from a formula:
The slope of a line can also be found just by using its formula. Below are two forms in which an equation can be written.
Slope intercept form:
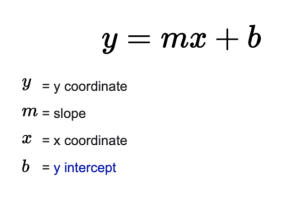
and point slope formula:

So, just by looking at the equations below, the slope can be found based on the position of the numbers and variables.
Example: In the equation y = 2x + 5, the slope of the line is 2.
Example: In the equation y – 5 = 4(x – 2), the slope of the line is 4.
If you’d like to learn about the 7 rules for exponents, click here.
