So, today we are going to talk about multiplication. But not the “regular” multiplication, like when you take 2 and multiply it by 3 to get 6. That kind of multiplication is the multiplication of integers, or two whole numbers. Today we are going talk about matrix multiplication, which is a whole different ballgame.
Let’s start with a brief review of matrices (singular: matrix). Broadly speaking, a matrix is defined as a set of numbers that are arranged in rows and columns. One example of a simple matrix is shown below:

We use big square brackets on both sides of the matrix, so that we can clearly see what numbers are part of the matrix. We characterize a matrix by the number of rows and columns it contains, so the matrix above would be called a “2 x 3 matrix” (two rows by three columns). Matrices can have the same number of rows and columns, which classifies them as a “square matrix,” or they can have different numbers of rows and columns. There are no limits to the numbers of rows and columns that are possible; as long as there is at least one row and one column, we call the set of numbers a matrix.
Why would I care about matrices, you may be wondering? Well, it turns out that matrices are useful in a whole variety of real-world settings. Essentially, any time you are working with a lot of numbers, and they can be characterized in rows and columns, it makes sense to think about using a matrix. In a very common example, people who design video games use matrices all the time to design and manipulate three-dimensional figures. In this kind of system, each position of the figure in space is represented by three numbers (X-, Y-, and Z-coordinates). This means that the overall location of the figure can be represented by a matrix, and moving the figure in space requires manipulating (mathematically) the matrix that you have set up!
Other examples where we use matrices in real life include in traffic control and design (trying, although not necessarily succeeding, to minimize traffic on the road); in medicine, when healthcare systems determine how to best diagnose and treat patients; and in cryptography, so people can send coded messages to each other without worrying about someone intercepting the message along the way.
Now that we understand that matrices can be useful ways to represent and manipulate lots of data, let’s talk about their mathematical operations. Most operations that we do with “regular’ numbers (addition, subtraction, and multiplication) can also be done with matrices. Interestingly, you cannot divide matrices like you do with regular numbers, for reasons which are beyond the scope of this post.
But even though we can add, subtract, and multiply matrices, each one of those operations is more complex than the analogous operation would be if we were working with single numbers.
Today we are going to focus on matrix multiplication.
First note: Unlike regular multiplication, matrix multiplication is not commutative. This means that even though in regular multiplication, 2 x 3 is the same as 3 x 2, and they both equal 6, matrix multiplication is different! For matrix multiplication, the order in which you write the two matrices matters.
Second note: In order to be able to multiply two matrices, the number of columns in the first matrix has to equal the number of rows in the second matrix. Otherwise, the multiplication cannot happen. Some examples below show when matrix multiplication is possible and when it is not:

In the top example, there are three columns in the first matrix and three rows in the second matrix, which means that matrix multiplication can occur. Neither of the other two examples fulfill the necessary criteria, which means that they cannot be multiplied.
Let’s focus on the first example. To do multiplication, we are going to multiply the first row of the first matrix by the first column of the second matrix
More specifically, we are going to multiply 2 (the first number in the first row of the first matrix) by 3 (the first number in the first column of the second matrix), 1 (the second number in the first row of the first matrix) by 1 (the second number in the first column of the second matrix), and 3 (the third number in the first row of the first matrix) by 7 (the third number in the first column of the second matrix), and add those values all together:
2*3 + 1*1 + 3*7 = 6 + 1 + 21 = 28
This number is going to be the first number of the first column of the new matrix.
We are then going to multiple the first row of the first matrix by the second column of the second matrix. Using the same logic, we get the following:
2*8 + 1*9 + 3*-5 = 16 + 9 -15 = 10
This number is going to be the first number of the second column of the new matrix.
Then we multiply the second row of our first matrix by the first column of the second matrix:
-2*3 + 0*1 + 5*7 = -6 + 0+ 35 = 29
This number is going to be the second number of the first column of the new matrix.
Finally, we multiply the second row of our first matrix by the second column of the second matrix:
-2*8 + 0*9 + 5*-5= -16 + 0 – 25= -41
This number is going to be the second number of the second column of the new matrix.
Our answer, therefore, is a matrix that looks like this:

Even though this felt kind of complicated, we can use a visual depiction of what we just did to try to make things easier:

A few important notes about matrix multiplication, before we do some practice examples.
- Note 1: The answer that we get form multiplying two matrices together is also a matrix. We call it the “matrix product” (because it is a matrix that is a product….), and it always has the same number of rows as the first matrix and the same number of columns as the second matrix.
- Note 2: We can also multiply a matrix by a regular number, which we call a “scalar.” We are not going to talk about this operation in detail, but it involves simply multiplying each element of the matrix by the same scalar number (like distributing the scalar to all components of the matrix).
- Note 3: There are several special matrices with unique properties. Two of them that may be relevant for our purposes are the “identity matrix” and the “zero matrix.”
- The identity matrix is a matrix where each element of the matrix is equal to 1. If you multiply any matrix by an identity matrix (assuming that the identity matrix has the correct number of rows and columns), your answer will be the original (i.e., non-identity) matrix.
- The zero matrix is a matrix where each element of the matrix is equal to 0. If you multiply any matrix by the zero matrix, your answer will be a matrix of all zeros.
Now for some examples! For each of the examples shown below, we are going to use the procedure that we outlined above in order to calculate the matrix product.
Example 1: What is the matrix product of the following two matrices?

Answer:
General strategy: We are going to multiple each row of the first matrix by each column of the second matrix.
- Step 1: First row of first matrix * first column of second matrix = 1*10 + 2*20 + 3*30 = 10 + 40 + 90 = 140
- Step 2: First row of first matrix * second column of second matrix = 1*11 + 2*21 + 3*31 = 146
- Step 3: Second row of first matrix * first column of second matrix = 4*10 + 5*20 + 6*30 = 320
- Step 4: Second row of first matrix * second column of second matrix = 4*11 + 5*21 + 6*31 = 335
- Step 5: Put these numbers into the correct positions in the new matrix (step 1 solution is top left; step 2 solution is top right; step 3 solution is bottom left; step 4 solution is bottom right):

Example 2: What is the matrix product of the following two matrices?

Answer:
General strategy: We are going to multiple each row of the first matrix by each column of the second matrix.
- Step 1: First row of first matrix * first column of second matrix = 3*3 + 4*6 = 33
- Step 2: First row of first matrix * second column of second matrix = 3*1 + 4*9 = 39
- Step 3: First row of first matrix * third column of second matrix = 3*5 + 4*7 = 43
- Step 4: Second row of first matrix * first column of second matrix = 7*3 + 2*6 = 33
- Step 5: Second row of first matrix * second column of second matrix = 7*1 + 2*9 = 25
- Step 6; Second row of first matrix * third column of second matrix = 7*5 + 2*7 = 49
- Step 7: Third row of first matrix * first column of second matrix = 5*3 + 9*6 = 69
- Step 8: Third row of first matrix * second column of second matrix = 5*1 + 9*9 = 86
- Step 9: Third row of first matrix * third column of second matrix = 5*5 + 9*7 = 88
- Step 10: Put these numbers into the correct positions in the new matrix:

Example 3: What is the matrix product of the following two matrices?

Answer:
General strategy: We are going to multiple each row of the first matrix by each column of the second matrix.
- Step 1: First row of first matrix * first column of second matrix = 1*7 + 2*8 + 3*9 = 50
- Step 2: Second row of first matrix * first column of second matrix = 4*7 + 5*8 + 6*9 = 122
- Step 3: Put these numbers into the correct positions in the new matrix (step 1 answer is the first row; step 2 answer is the second row):

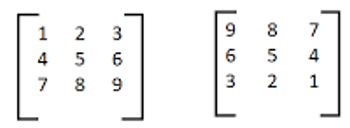
Example 4: What is the matrix product of the following two matrices?
Answer:
General strategy: We are going to multiple each row of the first matrix by each column of the second matrix.
- Step 1: First row of first matrix * first column of second matrix = 1*9 + 2*6 + 3*3 = 30
- Step 2: First row of first matrix * second column of second matrix = 1*8 + 2*5 + 3*2 = 24
- Step 3: First row of first matrix * third column of second matrix = 1*7 + 2*4 + 3*1 = 18
- Step 4: Second row of first matrix * first column of second matrix = 4*9 + 5*6 + 6*3 = 84
- Step 5: Second row of first matrix * second column of second matrix = 4*8 + 5*5 + 6*2 = 69
- Step 6: Second row of first matrix * third column of second matrix = 4*7 + 5*4 + 6*1 = 54
- Step 7: Third row of first matrix * first column of second matrix = 7*9 + 8*6 + 9*3 = 138
- Step 8: Third row of first matrix * second column of second matrix = 7*8 + 8*5 + 9*2 = 114
- Step 9: Third row of first matrix * third column of second matrix = 7*7 + 8*4 + 9*1 = 90
- Step 10: Put these numbers into the correct positions in the new matrix:

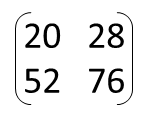
Example 5: What is the matrix product of the following two matrices?

Answer:
General strategy: We are going to multiple each row of the first matrix by each column of the second matrix.
- Step 1: First row of first matrix * first column of second matrix = 1*2 + 3*6 = 20
- Step 2: First row of first matrix * second column of second matrix = 1*4 + 3*8 = 28
- Step 3: Second row of first matrix * first column of second matrix = 5*2 + 7*6 = 52
- Step 4: Second row of first matrix * second column of second matrix = 5*4 + 7*8 = 76
- Step 5: Put these numbers into the correct positions in the new matrix (step 1 solution is top left; step 2 solution is top right; step 3 solution is bottom left; step 4 solution is bottom right):
Author: Mindy Levine, PhD
