Today we are talking about trigonometry, and in particular, talking about trigonometry techniques, trigonometry functions, and lots of interesting applications of trigonometry. Spoiler alert: trigonometry may not be your favorite topic, but it is used in so many real-world applications that it becomes imperative to learn and understand!
Let’s start with some definitions. Trigonometry, according to Britannica online, is defined as “the branch of mathematics concerned with specific functions of angles and their application to calculations.” What does this really mean? Essentially, it means that trigonometry has to do with the mathematics of triangles, and in particular, the angles of triangles and the relationships between those angles and the lengths of the triangles’ sides.
Trigonometry of Right Triangles
The first level of understanding trigonometry focuses exclusively on right triangles, which are triangles which have a 90-degree angle. For such triangles, we can define that the two shorter sides of the triangle are considered the triangle’s “lengths,” and the longest side is considered the triangle’s “hypotenuse.” The figure shown below provides an example of a right triangle, with the triangle’s lengths, hypotenuse, and 90-degree angle clearly delineated.

For a right triangle, we can define three trigonometric functions, or relationships between angles and the lengths of the triangle’s sides. These are called sine (abbreviated “sin”), cosine (abbreviated “cos”), and tangent (abbreviated “tan”), and are defined according to the equations shown below:
- Sin θ = opposite / hypotenuse
- Cos θ = adjacent / hypotenuse
- Tan θ = opposite/ adjacent
To understand what these equations mean, let’s focus again on a right triangle, but this time include an angle θ (which is one of the interior angles of the triangle that is not the 90-degree angle). For this angle, the sides of triangle can be differentiated into “opposite,” which is the side of the triangle that is opposite the angle θ, and “adjacent,” which is the side of the angle that is adjacent to the angle θ.
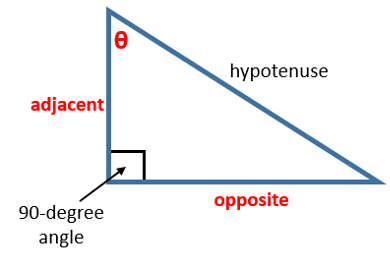
Once we understand this diagram, we can see how the trigonometric functions (“trig functions” for short) are actually amazing, since they relate the measure of an angle (in degrees, usually) to the lengths of the sides of a triangle which contains that angle. Pretty cool, right?
Sometimes it can be hard to remember these three trig functions, and so luckily we have a mnemonic, or acronym, that makes it easier. The mnemonic is: SOHCAHTOA.
SOHCAHTOA
What does this mean? Let’s break it up into three parts:
- SOH: sin = opposite/ hypotenuse
- CAH: cos = adjacent/ hypotenuse
- TOA: tan = opposite/ adjacent
So, is that it? That’s all the trig functions that we have? No!! There is more! In particular, there are three more trig functions that are related to the main trig functions, called cosecant (abbreviated “csc”), secant (abbreviated “sec”), and cotangent (abbreviated “cot”). The definitions of these functions are shown below:
- Csc θ = 1/ sin θ = hypotenuse/ opposite
- Sec θ = 1/ cos θ = hypotenuse/ adjacent
- Cot θ = 1/ tan θ = adjacent/opposite
It turns out that each of these new trig functions are actually related to one of the original trig functions, which makes it easier to remember.
Trigonometry of Other Triangles
Luckily for us, the study of trigonometry doesn’t end here. In fact, trigonometry techniques and calculations can be broadened to deal with non-right triangles, i.e., triangles that do not have a 90-degree interior angle.
How? Mathematicians developed the “law of sines” and the “law of cosines” to relate the angles of any triangle to lengths of their sides. We will discuss each of these laws in turn.
The “law of sines” says that we can relate the angles of any triangle to the side lengths of that triangle, by determining that the ratio of the sine of each angle to the length of the opposite side is constant. Sound confusing? Let’s look at a particular example.
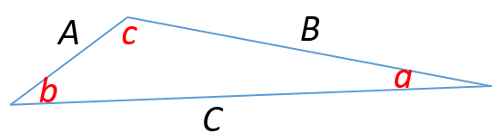
If I have a triangle with sides of lengths A, B, and C, which are opposite angles a, b, and c (as in the figure above), then the law of sines states that:

The “law of cosines” relates the cosine of the angles of any triangle to the lengths of the sides of that triangle, although the equations that comprise this law can look a little complicated.
Let’s consider the same triangle that we used above:

In this case, the law of cosines states that:
- A2 = B2 + C2 – 2BC*cos(a)
- B2 = A2 + C2 – 2AC*cos(b)
- C2 = A2 + B2 – 2AB*cos(c)
There are lots of other parts to trigonometry, including how we can use the unit circle to calculate common trigonometry functions, how we graph trigonometric functions, and how we understand and derive trigonometry identities. We’ll leave most of that for another day, and focus on an important question (or three questions, more accurately):
What is trigonometry good for? What are its applications? Why should we care about studying and understanding it?
Applications of trigonometry
It turns out that trigonometry functions are used in real life in all kinds of scenarios, including astronomy, navigation, and biology! Let’s discuss some specific examples:
Trigonometry in astronomy: Astronomy, or the area of science that deals with stars and all objects in space, needs trigonometry to calculate the distance to stars. How? Astronomers measure the position of a star one day, and then after a certain amount of time has passed, they re-measure the position of the same star. The star is going to look like it has moved, but really what has happened is that the astronomer has moved! More specifically, because of the rotation of the earth, there will be a different angle between the astronomer and the star after a certain amount of time has passed. Using information that is known about earth’s rotation, and knowledge of trigonometry, we can use the change in the viewing angle between the astronomer and the star to figure out how far away the star is from earth!
Trigonometry in navigation
People on ships in the middle of an ocean need trigonometry to figure out their location. In fact, this isn’t specific to ships or to oceans… anyone who is lost, in any location, can use the same trigonometry principles to figure out their location. How does this work? You need triangulation! What is triangulation, you might be wondering? It is related to our favorite geometric shape, triangles! What does it mean for navigation? It means that you can:
- measure the angle between your position and the sun (or moon, or stars),
- measure the angle that the sun makes with the horizon,
- use that information to figure out your distance from the sun, and
- calculate your precise location based on this distance.
Trigonometry in architecture and building
In these fields, we need a lot of trigonometry, to make sure that the buildings that are built don’t fall down and cause injury! We probably also want to design buildings that are aesthetically pleasing, and buildings that will last for a long time without breaking down. How do we use trigonometry in these fields? In one example, architects use trigonometry to figure out the optimal angles for a sloped roof, to make sure that the roof is steep enough for the rain and snow to fall off, but not too steep (because that can compromise the structural integrity of the building). Builders use trigonometry too, to make sure that a building’s angles and structure meet code regulations, for example, or in building bridges that are robust enough to withstand the load of millions of cars traveling on them each year.
In summary, the next time you drive over a bridge, or use your GPS navigation, or try to figure out the distance of the closest star in light-years (OK, some of these examples may be less relevant to your daily life) – remember to thank trigonometry for its role in enabling all of these activities!
Author: Mindy Levine
