Exponents division can be tricky. There are, however, a few rules you can follow that can make this difficult task formulaic! In this article we’ll cover how you can divide exponents with the same base.
We’ll show you the formula – we promise! But before this, let’s begin with an example in order to make sure you understand the principle behind the lesson – this will make applying the formula even easier.
Let’s start with a simple problem:
![]()
Let’s answer this the “conventional” way:
![]()
This can also be written like this:
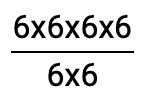
Now, we can simplify this by canceling out any repeat values in the numerator and denominator. In this case there are four “6’s” in the numerator and two ”6’s” in the denominator.
Therefore, the simplified fraction is as follows:
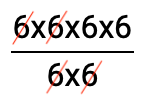
The final step would be to rewrite (6×6) in the form of an exponent:
![]()
Thus,
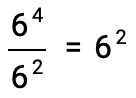
Of course, this is the LONG way of solving this problem. Did you notice, however, that

In other words, did you notice that if you subtract the value of the exponent in the denominator from the value of the exponent in the numerator, you get the value of the exponent of the solution? This is the formula.
Whenever you divide two exponents with the same base, you can subtract the value of the exponent in the denominator from the value of the exponent in the numerator.

Remember, this ONLY works if the exponents have the same base. If the value of the bases are different, this rule does not apply.
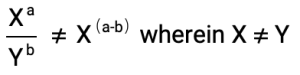
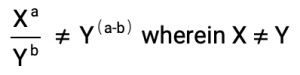
We’ll cover the rule for exponents division with different bases in another article!
