You may have heard about quadratic equations in your math class, or maybe in the hall listening to an older student talking about a new unit in math class…but…what is a quadratic equation? Quadratic equations are useful in modeling real world situations such as projectile motion, or modeling profit and loss for businesses, or the ideal dimensions for an space to achieve the maximum area. Let’s learn all about solving quadratic equations and take a look at some examples.
Solving Quadratic Equations: The Quadratic Formula
The standard form of an equation is the structure of the equation with letters in the positions where numbers would ordinarily go. The standard form of a quadratic equation is:
ax2 + bx + c = y
The letters a, b, and c are all constants, which are values that stay the same and are values that are known. To solve this equation, the goal is to find what the x-value is, given constant values of a, b, and c. The quadratic formula is one way to solve for x, but you can also find the correct x-value by either factoring the equation or graphing it.
The quadratic formula allows you to use the values of a, b, and c to solve for x when y is equal to zero:
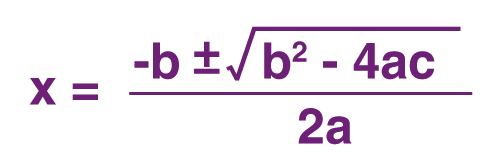
Practice Problem 1: A step-by-step guide to solving quadratic equations.
x2 – 9x + 14 = 0
Step 1: Identify a, b, and c.
a = 1
b = -9
c =14
Step 2: plug in the values for a, b, and c into the quadratic formula.
x = (- (-9) ± √(-9)2 – 4(1)(14))/2(1)
Step 3: Evaluate the equation.
You can do this step using either a calculator or pen and paper!
x = (9 ± √81 – 56)/2
x = (9 ± √25)/2
x = (9 ± 5)/2
x= 7 or 2
Graphs of Quadratic Equations:
The shape that is formed when graphing a quadratic equation is called a parabola. As you would any equation, quadratic equations can be graphed by plugging in values for x and calculating the y-value, and then graphing these coordinates. When you graph a quadratic equation, the solutions are the points where the parabola crosses the x-axis and are known as the x-intercepts.
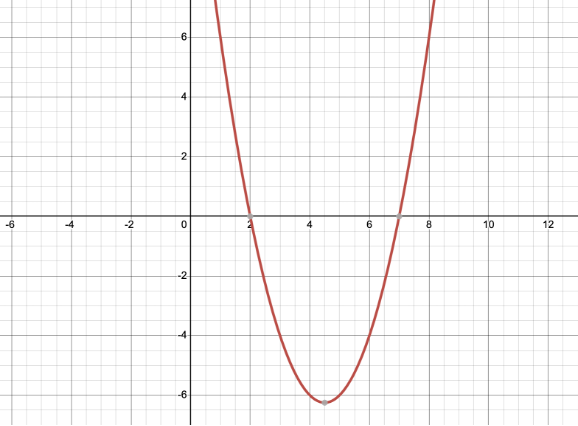
A practice problem to try yourself:
Practice Problem 2:
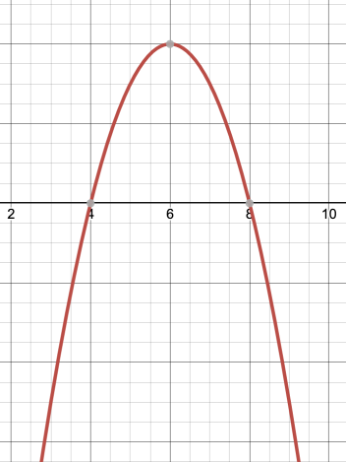
A football travels along a path represented by the quadratic equation:
-x2 + 12x – 32 = y
If y represents the height (in feet) and x represents the horizontal position of the ball (in feet), what is the horizontal distance between the footballs starting and ending position? Hint: find the solutions to the equation when y = 0 using the quadratic equation, and then find the distance between the two x-values.
Solution:
4 feet
Graph of the parabola from problem 2:
Author: Sydni Britton
